Chaos and Fractals
A short trip in fractional dimensions
[ Strange Attractors | Fractional Dimensions | String Systems | Nature | Software ]
| © CSE, 2003-2004 |
Strange Attractors
Chaos is an interesting behavior of systems that lies between the simplicity of stability or periodicity and the highest disorder of randomness. Such systems are unpredictable, but a hidden order is discernable.Examples of chaotic behaviors are frequently observed in iterated equation systems. Even in systems as simple as the logistic equation, a model that has been used since decades to simulate fluctuations of biological populations. The logistic equation stipulates that the relative population (1 represents the maximum possible population) at year t is dependant on the population in the previous year t-1 according to the expression:
Logistic Equation
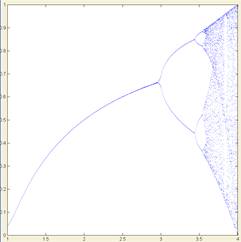
In the figure above, the population reached after 30 years and during the 50 following years (t = 30 to 80) is plotted versus the constant used in the equation. Up to a constantÝs value of 3, no surprise, an equilibrium population is reached (the population remain stable, one single 'dot' on the plot). For higher constants, oscillating behaviors begins, with a phenomenon known as period doubling. Finally, at high ranges, chaotic behavior can be observed.
However, one can see that this is non-random; it seems to have some order in the cloud of dots. Effectively, Feigenbaum discovered some underlying rules, such as the Feigenbaum constant that describes the period doubling.
In most iterated function systems, such behavior happens for certain values of parameters. It is common to observe that 90%-99% of the parameters' values lead to equilibrium or periodic systems, but that some sets of constants lead to chaotic behavior.
Obviously, in engineering systems, chaotic behavior must be removed as its sudden modifications of state can results in stress, or, in the case of chemical engineering, in violent modifications in the pressure and temperatures leading to explosive dangers.
Another example of iterated functions, this time in two dimensions - hence assigning to x and y values related to x and y as they were in the past - is the Pickover System:
y = sin(a*x)+d*sin(a*y)
For several values of the four constants, chaotic systems appears (in the plots below, subsequent values of x and y are plotted in the x-y plan. Equilibrium would appear as a single dot, a periodic behavior as a closed curve).
 a=2.15;b=1.75;c=0.89;d=1.4 |
 a=2.723;b=2.123;c=1.123;d=1.543 |
Other interesting systems include the quadratic map, where x and y are defined in quadratic terms. The complete quadratic map has 12 terms and hence 12 constants and similar behavior are observed:
 x = -1.2+0.7x2+0.1y+0.4y2 y = 0.4+1.1x+0.8x2+1.2xy-0.6y-1.2y2 |
 x = 1+0.1x-1x2+0.6xy-0.1y-0.7y2 y = -0.1-0.6x-0.4x2-0.5xy-0.6y-0.1y2 |
Obviously, such behaviors also happen in 3-dimensional systems. The best known system is the iterated differential equation system of Lorenz, which describes a system evolving with time similarly to the logistic equation above. The state of the system orbits around two fixed points, but it is unpredictable when it will switch from one orbit to the other. This is called a strange attractor.
Such systems are best observed dynamically, the movement of the system being quasi hypnotic due to the frequent changes of state.
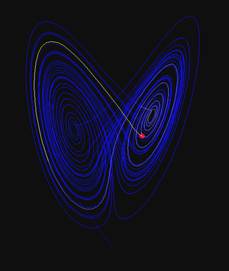 Lorenz Attractor: dx/dt = 10(y-x) dy/dt = x(28-z)-y dz/dt = xy-2.85z |
 Rössler Attractor: dx/dt = -(y+z) dy/dt = x + 0.2y dz/dt = 0.2 + xz ˝ 8z |
If chaotic behavior can be observed in mono-dimentional (logistic equation) as well as in two and three dimensional (quadratic map, lorenz attractor) systems, it is no surprise that it appears also when dealing with complex numbers by any mapping (a function of a complex number) that transforms a complex number in a real number.
For instance, the well-known Newton-Raphson algorithm is used to find the roots of a function (e.g. for which values of the complex number z is z3 equal to -1?). If several solutions are possible, one can map the complex number to its attractor, i.e. the solution of the function it leads to (if it leads to solution #1, its value is 1). All complex numbers leading to the same solution (i.e. having the same map) define the bassin of attraction of this solution. By plotting the different basins of attraction with different colors, regions with highly complex boundaries are revealed.
 z5=1 |
 z7-3z5+2z3-5z=1 |
These boundaries show an interesting property: the complexity remains constant however closely it is observed. This means that the closer the zoom, the more details appear ˝ in other word, the more precisely we measure the length of boundary, the longer it is!
Fractional Dimensions
This property is somewhat strange. If one measures the width of the browser window twice, once with a ruler of 1 cm and another time with a ruler of 10 cm, the same width will be measured. The Newton-Raphson boundaries, however, are longer if measured with smaller rulers...This observation led to the definition of a new, fractional, definition of the dimension of a figure. Hausdorff defines the dimension as being the logarithm of an objectÝs size in function of the logarithm of the rulerÝs size, while reducing the ruler toward zero. For instance, the dimension of a straight line, or of the width of your browser's window, is obtained as follow:
Measuring a 1 meter long line with a 1 meter ruler gives a length of 1; measuring with a ruler of 50 centimeters gives a length of 2. Hence the dimension is ln(2)/ln(2) = 1. The dimension of a square is similarly given by using a ruler of 1 meter, leading to 1 by 1, and then a ruler of 0.5 meter, leading to measures of 2 by 2. Hence the dimension is ln(4)/ln(2) = 2.
In some cases, however, the dimension will not be an integer number. In the boundaries of the basin of attraction of NewtonÝs method, the smaller the ruler, the longer the curve, hence the dimension of the curve is larger than 1.
This is best illustrated by simpler figures. Take for instance KochÝs curve. KochÝs curve is generated by an iterated Lindenmayer System, a string replacement system (see below for more information). Some initial iterations are shown below:
 First Iteration |
 Second Iteration |
 Fourth Iteration |
When measuring the curve with a "long" ruler, some details will not be measured. If you think that this is just a question of precision, have a look at the last figure - what you see is limited by the precision of your monitor. If you measure the curve on your screen, you will ignore all details smaller than one pixel. To estimate the dimension of Koch's curve, one stipulates that rulers cannot measure details smaller than they are. Each subsequent curve is composed of 4 segments of size 1/3 of the previous ones. Hence when the ruler is thrice as small, the length increase of a factor 4. Hence the Koch curve has a dimension of ln(4)/ln(3) = 1.261.
Benoît Mandelbrot coined a new world: fractals, for figures whose Hausdorff dimension strictly exceeds the topological dimension. In the case of KochÝs curve, the topological dimension is 1 (it is a curve), and hence this curve is a fractal.
Mandelbrot defined a new mapping of the complex plan (the Mandelbrot Set) by including all complex points that do not diverge to infinity when iteratively squared and added to the initial point: zi+1 = zi2 + z0. The boundary of the surface thus defined has the peculiar property of having a Hausdorff dimension of 2 while it has (it is a curve) a topological dimension of 1. Mandelbrot SetÝs complexity actually increases when zooming in!
 Whole Set (-2-1.5i:1+1.5i) |
 -.083-0.25125i:-0.7175-13875i |
 -0.81453-0.17602i:-0.80989-0.17138i |
 -0.81227-0.17286i:-0.81209-0.17268i |
 -0.81225-0.17281i:-0.81224-0.17280i |
 -0.8122469-0.1728018i:-0.8122466-0.1728014i |
The fourth detail is 600 trillion times smaller than the whole set ("trillion" is taken in its US signification: there is space for 6*1014 images of the size of the last one in the initial one), but the complexity is still increasing...
Another frequent feature of fractals can be observed in the sequence of zoom in the Mandelbrot Set shown above: a self similarity ˝ similar shapes are found at different scales. In the last image appears a shape similar to the whole Mandelbrot Set, but it is slightly different and its length is 25 million times smaller!
At the extreme of self-similarity are fractals invariant with scale. Among them lie the Julia sets that are similar to the Mandelbrot set ˝ a mapping of the complex space, but with a slightly different equation: zi+1 = zi2 + c where c is a complex constant.
Due to the invariability, zooming in Julia set is less interesting, but since there are as many Julia Sets as there are complex numbers, a sufficient large number of Julia Sets can be observed to satisfy the most curious explorer.
As a side note, the mathematician Julia who gave his name to those figures researched them in the beginning of the century and studied those figures by hand. One of the figures below require approximately 12 millions complex multiplications, so you can imagine that Julia must have been quite quick in head-calculations, even if he had time while lying in the war-hospital! Note that the whole theory of chaos is largely posterior to Julia's work - Mandelbrot, that systematized this new science did it in the seventies.
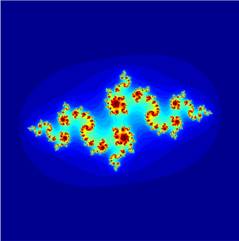 c = -0.845+0.24375i |
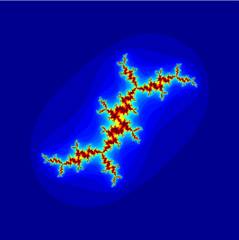 c = -0.08+0.85i |
Note that, from a mathematical point of view, only the ensemble itself (in black) is interesting, as it is its boundary that has a Hausdorff dimension of 2.
For aesthetic reasons however, colors have been added in function of how many iterations are required before divergence to infinity occurs (infinity being considered equal to 2 in this situation, as it is mathematically proven that any complex number larger than 2 will diverge). Instead of colors, such highlighting can be pictured as an altitude, and pseudo 3D pictures can be realized and rendered.
Note that the same phenomena happen for most functions of the complex plan, hence similar (albeight graphically very different) figures can appear if other iterative functions are chosen.
 Mandelbrot Set (-1.2725+0.18i:-1.1225+0.33i) |
 Map based on 2*z*z0*tan(pi/z) (0.21-0.5813i:0.39-4013i) |
However, fractals can be generated with higher dimensions. A common way is to use hypercomplex numbers, for instance the 4-dimensional quaternions. Quaternions are rather similar to complex numbers, with 3 imaginary dimensions added to one real dimension: z = a+bi+cj+dk, where i, j and k are different "square roots" of -1; quatrenions are defined with the following rules (note that the multiplication is not commutative): i2=j2=k2=-1, ij=-ji=k, jk=-kj=i, ki=-ik=j. Julia and Mandelbrot sets can be generated. As they are 4D objects, and as it is rather difficult to plot four dimensions on the 2D surface of a computer-screen, one dimension must be fixed and the resulting fractal is a 3D object that can be rendered. The fourth dimension can of course be modified to create sequences of 3D objects (movies).
Below are some extract from a sequence of Quaternion Julia Sets, with a constant of 0.5+0.4i+1j+0.05k. The fourth dimension is the "time" and is fixed in each picture. It evolves from 0.2 to 1.1 in the four snapshots shown below:
 Time = 0.2 |
 Time = 0.5 |
 Time = 0.8 |
 Time = 1.1 |
String Systems
While these curves are most interesting to observe (and the reader is strongly encouraged to do so), the study of fractional dimensions is easier with Lindenmayer Systems. Such systems are string rules, stating for instance that the string ýFţ is replaced by ýF-F++F-Fţ. This substitution is conducted iteratively on an initial string (for instance ýFţ). The resulting string is graphically interpreted; F means ýDraw a lineţ, + and ˝ indicate turning of some angle. The system described above defines the Koch curve seen above. With an initial string of ýF+F+F+F+Fţ, it leads to the Koch Island, which has the funny property of having an infinite perimeter ˝ the perimeter being of dimension larger than 1, as seen above - that enclose a finite surface!By using rules of higher complexity, more complex figures can be drawn, such as the well known Sierpinsky triangle (of dimension around 1.585; if you divide the ruler's size by two, you measure for each triangle existing at iteration i twice the number of sides (6) + 3 new sides that "appear" as a new triangle inside the older triangle. So you measure 9 instead of 3 (ancient triangle) with a ruler shorter by a factor 2. ln(9/3)/ln(2)=1.58496...).
 Koch Island |
 Sierpinsky Triangle |
Such system can be drawn in three dimensions, such as the Menger Sponge of dimension 2.727 (=ln(20)/ln(3): 20 little squares when the ruler is 3 times smaller):

Menger Sponge
Imitating the nature
As a final comment, the nature is filled with objects of fractional dimensions ˝ from the coast of England (which is longer when the ruler is shorter - do you think anybody ever estimated the length of the coast while taking each rock, or even each grain of sand into consideration?) to plants and trees. Fractal drawing techniques can hence be used to create natural-like objects.Iterated function systems can be used to draw plant-like objects such as ferns, Lindenmayer systems are used to emulate plant growth and obtain rather realistic models of trees.
 BarbsleyÝs Fern |
 Fractal Tree |
Finally, a class of fractal that has not been mentioned yet is the "folded plan". A plan is of dimension 2. When it is folded like aluminium foils, its dimension increase between 2 and 3. Hence such objects are fractals. With adequate coloring, such folded plans can be used to create rather realistic landscapes, for instance by adding a cut-off value for the sea level. Similarly, looking at the plan from above and using the altitude as an intensity map, clouds-like shapes can be obtained.
These techniques can be combined to obtain realistic landscapes, but this goes beyond the chaos theory... Breathtakingly realistic landscapes in conjunction with ray-tracing techniques are used frequently in your favorite SF moviesÍ
 Folded Plan |
 Fractal Landscape |
 Fractal Clouds |
 "Artificial" combination |
Subjective Reference List
Sorry, my intensive study of this field goes back to the beginning of the nineties of the preceding millenium, so this bibliography is not updated with the most recent books... The list is alphabetically sorted by first author.- M. Barnsley, Fractals everywhere, Academic Press Inc., 1988
- J. Feder, Fractals Plenum Press, New-York, 1988
- J. Gleick, Chaos, The Viking Press, New York, 1987
- B. Mandelbrot, Les objects fractals, Flammarion, Paris, 1975
- B. Mandelbrot, Fractals: Form, Chance and Dimension, Freeman & co., San-Francisco, 1977
- B. Mandelbrot, The fractal geometry of nature, Freeman, New-York, 1985
- H.-O. Peitgen & P.H. Richter, The beauty of fractals, Images of complex dynamical systems, Springer-Verlag, New-York & Berlin, 1986
- H. Peitgen, H. Juergens & D. Saupe, Fractals for the classroom, Springer-Verlag, New-York & Berlin, 1992
- P. Prusinkiewicz 6 A. Lindenmayer, The algorithmic beauty of plants, Springer-Verlag, New-York & Berlin, 1990
- P. Prusinkiewicz & J. Hanan, Lindenmayer Systems, Fractals and Plants in Lecture Notes in Biomathematics vol.79, Springer-Verlag, New-York & Berlin, 1989
- D. Ruelle, Chaotic evolution and strange attractors, The statistical analysis of time series for deterministic nonlinear systems, Cambrige University Press, Cambridge, 1989
- R. Stevens, Fractals programming in C, M&T Publishing, 1989
- Fractal FAQ
CSE Fractals III
All images in this document have been created with the Malab program CSE Fractals III written by L.Cavin. This program can be downloaded here for free.Features and Usage
Callfractal_explorer; without any arguments. This command will open the main window and draw the Mandelbrot Set. All features are available via the menus.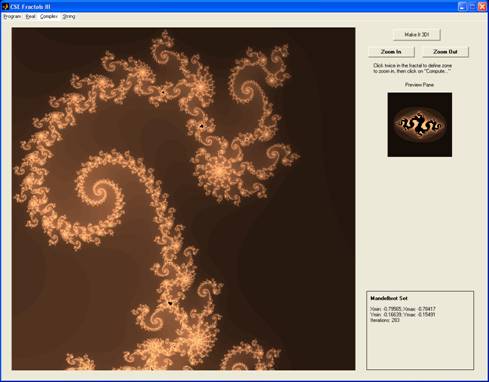
The features include:
- Logistic Equation1
- Real 2D Attractors:
- Henon Attractor1
- Pickover System1
- Arbitrary Quadratic Map1
- Real 3D Attractors:
- Lorenz Attractor2
- Rössler Attractor2
- Limited Quadratic Map2
- Complex Maps:
- Mandelbrot Set1,5
- Julia Sets1,3,5
- Arbitrary Polynomial Newton-Raphson Attraction Basins1,5
- Barnsley's Tree1,5
- Arbitrary Mandelbrot and Julia-based Sets1,5
- Quaternions:
- Mandelbrot and Julia Sets2
- String Systems:
- Lindemayer Systems Single Rule
- Lindenmayer Systems Multiple-Rules
- Plant-like systems:
- Barbsley's Fern4
- Fractal Trees
- 3-D Systems
- 3D-Multi-rules Lindenmayer Systems2
- Menger Sponge2,4
- Folded Plans:
- Fractal Clouds
- Fractal Landscapes2
1 Interactive Zooming
2 Interactive 3-D View
3 Julia explorer with on-the-fly previews
4 Limited to built-in parameters
5 Include the function Make-It-3D˘
|
For many functions, dialogs will allow introducing user-defined parameters for the calculation. Most dialog contains a button labeled "Cool Params" or "Examples" - this will propose a set of parameters leading to a chaotic behavior (as it is sometimes difficult to find a good parameter set), or displaying well-known systems or interesting results. Some example are also provided to highlight options not explicitely explained in the dialogs... For the computation of Julia Sets, it is of course possible to enter the Julia Constant by clicking on the main figure if it displays a Mandelbrot Set. |  |
Zooming is done by selecting the two bounds on the main figure (for complex sets, the button "Zoom In" must be pressed first).
Version and download
Version 1.0 - 26.07.04 [Legal Stuff]Download the function as a matlab .m file (188 Kb).
Download the function as a .zip file (33 Kb).
Limitations/Prerequisites
None known. Tested exclusively with MatLab R13.Proof of divergence:
This proof is given here, because most books and web sites mention the cutoff at a magnitude of 2 without further information...
The aim is to prove that any complex number z larger than 2 (the magnitude |z| is larger than 2) does not belong to the Mandelbrot Set. This means proving that |z2+c| is always larger than |z| if |z| > 2. In this case, the magnitude will increase at each iteration and the number will diverge to infinity when iterated on the equation z = z2+c.
Suppose an imaginary number z = a + bi.
The magnitude of z is: sqrt(a2+b2).
The square of this number is: z2=a2-b2+2abi;
The magnitude of z2 is: sqrt((a2-b2)2+4a2b2).
= sqrt(a4-2a2b2+b4+4a2b2) = sqrt(a4+2a2b2+b4) = sqrt((a2+b2)2)
Hence |z2| = |z|2.
From Hypothesis, |z| > 2, hence |z2| = |z|*|z| > 2*|z|.
From the vectorial addition, we know that |z2+c| >= |z2| - |c|
So if |c| <= |z|, |z2+c| >= |z2| - |c| > 2*|z| - |c| > |z|.
What if |c| is larger than |z|? Well, by hypothesis, |z| > 2 so |c| is also larger than 2. But z0 = c (initial iteration). So in the first iteration, |c| = |z| and both are larger than two, hence the conditions for divergence proven above are verified. The number will diverge to infinity. Hence only for |c| < 2 can the point z0 be in the Mandelbrot Set.
QED
Quick remark:
Might a smaller threshold for |z| be a sufficient condition?
Well, let's take the real number -2, in complex form -2+0i. Its magnitude is equal to 2 (square root of -22).
Applying the iterative Mandelbrot equation results in:
z0 = -2, c = -2
z1 = z02+c = -22-2 = 4-2 = 2
z2 = z12+c = 22-2 = 4-2 = 2
z3 = z22+c = 22-2 = 4-2 = 2
This is a fixed point, where zi+1 is equal to zi2+c. There is no divergence, hence the number belongs to the Mandelbrot set.
There is at least one number for which |z| = 2 that belongs to the set (this is by the way the only one), hence no threshold smaller or equal to 2 is possible.
Legal blahblah & Conditions of use
© CSE - L.Cavin, 2003, 2004
These libraries and functions (THE PROGRAM) are provided "as is" without warranty, either expressed or implied, including, but not limited to, the implied warranties of merchantability and fitness for a particular purpose. The entire risk as to the quality and performance of the program is with the person downloading or running the program (THE USER). Should the program prove defective, the user assumes the cost of all necessary servicing, repair or correction.
In no event will the Author or the Copyright holder be liable to the user for damages, including any general, special, incidental or consequential damages arising out of the use, peruse or inability to use the program (including, but not limited to loss of data or data being rendered inaccurate or losses sustained by the user or third parties or a failure of the program to operate with any other programs), even if the Author or the Copyright holder has been advised of the possibility of such damages.
The fact of downloading or running the program implies acceptation of the present liability limitation by the user.
These libraries and functions are free to use for non-commercial purposes and can be distributed (free of charge) as long as the copyrights notices are kept intact. In particular, if the program is distributed further by the user, the user is responsible for including this legal warning and liability limitation to the distribution.
It is also encouraged to improve these functions; please send to the author any improvements - we may want to include them in this distribution under the same conditions.
Do not be afraid, I am confident that the program will work - without warranties of course ;-)
Thanks to the Free Software Foundation for inspiring this nice little legal blahblah... My favorite part is the "inability to use"... even if the "general, special, incidental or consequential" part is also quite fun!
Page © Cavin Softwares Engineering, 2003-2004.
[last updated: 19.07.04]